秘書問題の最適解とは?37%の法則と現実への応用?37%の法則!最良の選択のための戦略
人生の選択を最適化!秘書問題を通して、最良の選択をするための確率論的戦略を学びましょう。37%ルールで有名な最適停止問題から、物件選び、理想のパートナー選びまで、幅広い意思決定に応用できる考え方を解説。数学的モデルと現実世界の制約、そしてさらなる探求への道筋を示します。あなたの選択を確かなものにする、知的冒険への招待です。
秘書問題の数学的背景とモデル
秘書問題、4つのモデルとは?確率最適化、具体的に何?
最適停止問題、無情報・完全情報モデルなど。
秘書問題の背後にある数学的背景を理解することは、問題の本質を深く理解するために不可欠です。
この章では、その数学的モデルや、様々な解法を解説します。

✅ 本書は、秘書問題の中でも最良選択問題を中心に扱い、直感的な理解を重視して解説しています。理系学部で学ぶ程度の知識があれば理解できます。
✅ 本書では、無情報型、完全情報型、期間問題など、様々な秘書問題のモデルを紹介し、Sum–the–odds定理やPPPといった高度なテーマにも触れています。
✅ 秘書問題は最適停止問題の一種であり、その解法や、nを大きくしたときの特性値の挙動など、興味深い問題設定とエレガントな解が特徴です。
さらに読む ⇒コロナ社 科学技術と共に歩む出典/画像元: https://www.coronasha.co.jp/np/isbn/9784339028409/無情報型、完全情報型、期間問題…色々なパターンがあるんですね!理系の知識があれば理解できるということなので、頑張って勉強してみようかな。
秘書問題は、確率最適化の一種である最適停止問題の具体例であり、その解法は、微分積分と応用確率論の知識で理解できます。
本書は、最適化基準と利用可能な情報の組み合わせに基づいた四つの主要モデル(無情報型最良選択、無情報型順位最小化、完全情報型最良選択、完全情報型順位最小化)を提示し、Sum–the–odds定理やFergusonの秘書問題、応募者総数nが未知の場合、期間問題など、多岐にわたるモデルを解説しています。
また、PPP(planarPoissonprocess)によるアプローチも紹介しています。
数学的な話はちょっと難しいけど、最適解を導き出すための考え方って、色んなことに役立ちそうだよね。なるほど~って感じ。
現実世界への適用と注意点
秘書問題、現実で使うと落とし穴?37%ルールは万能?
心理的・現実的要因で、37%ルールは限定的。
秘書問題の理論を現実世界に適用する際には、いくつかの注意点があります。
この章では、その点を詳しく解説し、より実践的な視点を提供します。

✅ 秘書問題は、候補者の中から最良の人物を選ぶ確率を最大化するための最適停止問題であり、特定のルールに従って選択を行う戦略を提示している。
✅ 最適戦略は、最初の一定数の候補者を見送り、それ以降の候補者の中でそれまでの最高評価者よりも良い人物が現れたら採用するというもので、「37%の法則」として知られている。
✅ 記事は、秘書問題のバリエーションである「順位最小化問題」や、現実の選択における行動傾向、および問題の前提条件が現実世界で必ずしも完全に満たされない点についても言及している。
さらに読む ⇒ シンクタンクならニッセイ基礎研究所 出典/画像元: https://www.nli-research.co.jp/report/detail/id=53168?site=nli人が早めに決断する傾向がある、とか、応募者の拒否とか、色々な現実的な問題があるんですね。
37%ルールが万能ではない、というのは、覚えておかないといけませんね。
秘書問題の最適戦略は、現実世界に適用する際にいくつかの注意点があります。
まず、人は早めに決断を下す傾向があり、最良の応募者が最初の見送り区間に含まれる場合、最後の応募者を選ぶことになり、結果として全体の平均的な順位の候補者を選ぶことになります。
また、現実には、応募者の拒否や、複数段階の選考プロセスが存在するため、秘書問題の前提条件が完全に満たされることは稀です。
心理的、経済的な要因も考慮すると、37%ルールが常に完璧に機能するわけではありません。
この理論はnが小さい場合には適用できないこと、そして調和級数に関する補足情報も考慮する必要があります。
37%の法則も、万能じゃないってのは、肝に銘じておかないとな。現実世界は、そんなに単純じゃないってことだね。面白い。
さらなる探求と応用
秘書問題、現実の意思決定に怎么活かす?
基本的な制約を考慮し、更なる探求を。
本書で紹介した秘書問題の基本的なケースに加えて、さらなる探求や、この問題の応用について考察します。
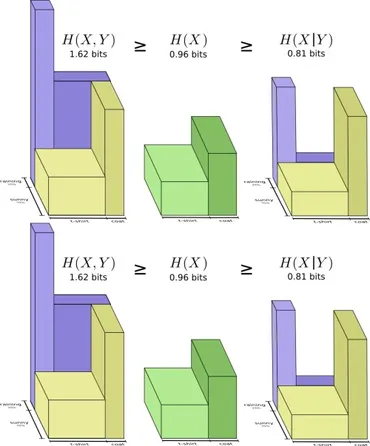
✅ 異なる確率分布を持つBobとAliceが、それぞれのコードを用いてコミュニケーションを取るときのメッセージの長さの違いを、交差エントロピーを用いて説明しています。
✅ 交差エントロピーH_p(q)は、分布qのメッセージを分布pのコードで符号化する際の平均的な長さを表し、H_p(q) ≠ H_q(p)のように、その値は非対称になります。
✅ 交差エントロピーは、2つの確率分布の違いを測る指標となり、分布が異なれば異なるほど、相手の分布に対する交差エントロピーは大きくなることが示されています。
さらに読む ⇒POSTD出典/画像元: https://postd.cc/visual-information-theory-3/37%の法則って、ほんとに奥深いですね!色んな場面で応用できそうだし、もっと勉強してみたくなりました。
秘書問題は、数学的にエレガントな解を持つ、確率論における興味深い問題です。
本書で紹介された内容はあくまで基本的なケースであり、現実の選択問題に適用する際には、これらの制約を考慮する必要があります。
本書を読み終えた読者には、さらなる探求のためにGilbert and Mosteller (1966)の論文が推奨されています。
秘書問題は、物件選びや理想の相手選びなど、さまざまな場面で意思決定を支援する考え方を提供します。
いや〜、面白かった!色んなことに応用できる考え方だね!
37%の法則、面白かったですね!数学的な理論が、現実世界の問題解決に役立つなんて、驚きです。
色々な場面で応用できるってことなので、もっと勉強してみようと思いました。
💡 秘書問題は、最適な選択を行うための数理的な問題であり、37%の法則がその解法として知られています。
💡 現実世界への適用には注意が必要であり、様々な要因を考慮する必要があります。
💡 この問題は、物件選びや理想の相手選びなど、様々な場面で意思決定を支援する考え方を提供します。


