複利って本当に効果あるの?複利の仕組みとは!?
💡 複利は利息が元本に積み立てられる仕組みです。
💡 複利は単利と比べて、時間が経つほど資産が増加します。
💡 72の法則を活用することで、複利で資産が2倍になる期間を計算できます。
それでは、第一章から詳しく見ていきましょう。
複利の仕組みと効果
では、早速ですが、複利の仕組みについてご説明します。

✅ この記事では、複利とは何か、単利との違い、効果的な活用方法について解説しています。
✅ 複利は、利益を元本に再投資することで、利益が利益を生み出す仕組みであり、長期間運用することで単利よりも効率的に資産を増やせることが説明されています。
✅ 記事では、複利計算に必要な「72の法則」を紹介し、資産が2倍になるまでの期間や目標利回りなどを計算する方法が示されています。
さらに読む ⇒ 三菱UFJ銀行出典/画像元: https://www.bk.mufg.jp/column/keizai/b0050.html複利は、長期投資で大きな力を発揮するんですね。
複利とは、利息が元本に加算され、その新しい総額に基づいて次の期間の利息が計算される仕組みです。
このプロセスが繰り返されることで、利息が元本に再投資され、利息が利息を生む「雪だるま式」の効果が生まれます。
単利は元本にのみ利息が付くのに対し、複利は利息にも利息が付くため、時間の経過とともに複利の方が大きな資産に成長します。
複利の計算方法は以下の公式を用います。
最終資産額 = 元本 × (1 + 利率) ^ 期間例えば、10000円を年利5%で10年間投資した場合、複利では最終資産額は約16289円となり、単利の15000円よりも1289円多くなります。
この差は、時間が経過するほど大きくなるため、長期投資において複利は非常に強力なツールとなります。
投資を行う際には、単に利益を追求するだけでなく、複利の力をどのように活用するかを考えることが重要です。
複利の力を理解し、長期的な視点で投資を行うことで、資産を効率的に増やすことができます。
複利って、すごいですね!
複利と単利の違い
続いて、複利と単利の違いについてお話しします。
公開日:2021/07/31

✅ 記事は、複利と単利の違い、そして複利の力について解説しています。
✅ 特に、長い期間での複利の効果は大きく、元本が雪だるま式に増えていくことを説明しており、アインシュタインが「人類最大の発明」と呼んだことにも触れています。
✅ 最後に、複利効果で運用できる投資商品として、分配金の再投資型投資信託を紹介し、長期投資の重要性を強調しています。
さらに読む ⇒株式会社FPブランディング FP Branding 出典/画像元: https://fpbranding.co.jp/magazine/compound-interest/なるほど、複利と単利の違いがよくわかりました。
複利とは、運用で得た利益を元本に加えて再投資し、その合計金額をもとに利益を得る方法です。
単利は元本のみで運用するため、複利のように利益が利益を生むことはありません。
複利は「利益が利益を生む」仕組みであるため、長期的に運用することで効率よく資産を増やせるメリットがあります。
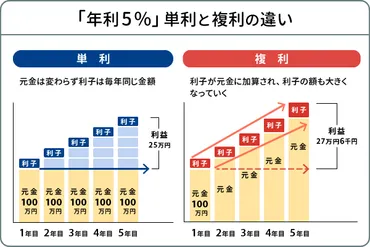
複利と単利の違いを理解するために、元本100万円を年利5%で5年間運用した場合の比較を挙げます。
単利では総額25万円の利益を得るのに対し、複利では総額約27万6000円の利益が得られます。
複利では毎年利益の金額が増加していくため、運用期間が長くなるほど利回り、つまり利益の差が大きくなります。
複利って、難しそうだけど、簡単なんだね!
複利効果を計算する「72の法則」
では、複利効果を計算する「72の法則」についてご説明します。
公開日:2022/01/05
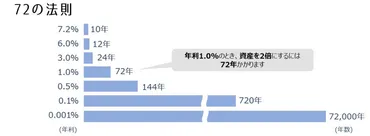
✅ 72の法則とは、複利で運用した場合にお金が2倍になるのにかかる期間を計算する便利な法則です。計算式は「72 ÷ 運用利回り(%) = 資産を倍にするのに必要な年数(年)」で、運用利回りと倍になるまでの年数を入れ替えることで、資産を倍にするのに必要な利回りを求めることもできます。
✅ 記事では、普通預金、定期預金、個人向け国債、債券、株式の例を用いて、それぞれの金融商品における72の法則の適用と、資産が倍になるまでの年数を示しています。特に、普通預金の金利が低いことから、銀行に預けても資産がなかなか増えないことがわかります。
✅ 72の法則は2倍だけでなく、3倍や4倍にするための計算式も存在します。3倍にするには115、4倍にするには144という数字を用います。記事では、利回り5%の金融商品で運用した場合の例を示し、資産が2倍、3倍、4倍になるまでの年数を計算しています。
さらに読む ⇒Dynamic Creation合同会社|代表 河原后里|お金とココロの両輪で豊かに出典/画像元: https://misatokawahara.com/rule-of-72/72の法則は、複利の効果を簡単に計算できる便利な方法ですね。
複利効果を計算する際に便利な「72の法則」は、資産が2倍になるまでにかかる年数を計算するものです。
たとえば年利5%で複利運用すると、「72÷5=14.4年」で資産が倍になります。
複利運用では、目標とする金額にどれくらいで到達できるのか、どれくらいの利回りが必要なのかを計算することが重要です。
ただし、利回りが変動すれば、運用成果にも変化が生じることを理解しておく必要があります。
単利の場合、資産が2倍になるまでの期間は「100÷金利(年利)」で計算できます。
年利5%で運用すると「100÷5=20年」となり、複利の場合と比べて約6年長くなります。
「72の法則」を活用すると、利回り別に資産が2倍になるまでの期間を簡単に計算できます。
たとえば年利3%、5%、7%で複利運用した場合、資産が2倍になるまでの期間はそれぞれ24年、14.4年、10.3年となります。
複利の効果は運用期間と利回りに大きく左右されます。
長期のマネープランを立てる際には、「72の法則」を活用して、目標金額達成までの期間や必要な利回りを計算することが有効です。
72の法則は、投資家にとって必須の知識だな!
複利運用と単利運用の比較
続いて、複利運用と単利運用の比較についてお話しします。
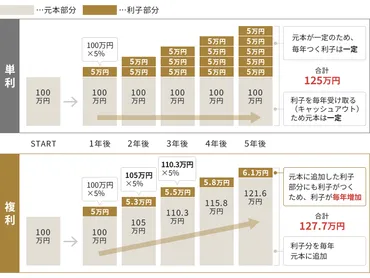
✅ 単利と複利の違いは、利子の計算方法です。単利は元本に対してのみ利子が発生しますが、複利は発生した利子を元本に組み入れ、利子の計算に含めるため、運用期間が長くなるほど利子が増えていきます。
✅ 複利効果を期待できる資産運用方法として、NISAとiDeCoが挙げられます。NISAの「つみたて投資枠」は、分配金を再投資することで複利効果が期待できます。iDeCoは、原則60歳まで解約できないため、分配金や運用益が再投資され、複利運用が期待できます。
✅ 複利の仕組みを理解し、効果を最大限に活かすことで、資産運用でより多くの利益を得ることが期待できます。金融庁の資産運用シミュレーションツールを活用することで、複利効果のイメージを掴み、資産運用計画を立てるのに役立ちます。
さらに読む ⇒MONEY VOYAGE出典/画像元: https://money-voyage.mizuho-sc.com/articles/41複利運用は、長期投資に適しているんですね。
複利運用は、発生した利息を元金に組み入れて運用する方法です。
利息が元金に組み入れられることで、利息が新たな元金として運用され、時間の経過とともに資産が増えていきます。
一方、単利運用は、発生した利息を元金に組み入れずに運用する方法で、元金は増えません。
複利運用は、単利運用よりも積立スピードが早く、将来必要となる資金を確保しやすいため、長期運用に適しています。
複利計算は、元金、金利、利息発生期間によって異なる結果が得られます。
利息発生期間が短いほど、資産はより早く増えます。
複利運用では、元金が時間とともに増え続けるため、単利運用よりも多くの利益を得ることができます。
複利運用は、魅力的だけど、リスクもあるから注意が必要よね。
複利運用のメリットとデメリット
最後に、複利運用のメリットとデメリットについてご紹介します。
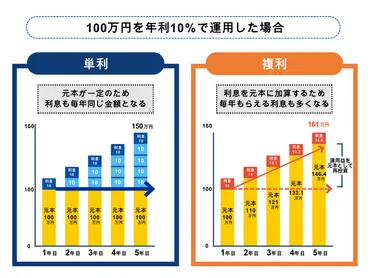
✅ この記事は、複利の仕組み、単利との違い、複利の効果について解説しています。
✅ 複利は利息に対してさらに利息がつく運用方法であり、単利と比較して資産を大きく増やすことができることを説明しています。
✅ また、複利の計算式を紹介し、具体的なシミュレーションによって、複利の効果が長期運用においていかに大きいかを示しています。
さらに読む ⇒七十七銀行出典/画像元: https://www.77bank.co.jp/financial-column/article58.html複利運用には、メリットとデメリットがあるんですね。
複利運用には、積立スピードが速い、将来必要となる資金を確保しやすいなどのメリットがある一方で、元金が減ってしまうリスクもあります。
複利運用のメリットとデメリットを理解した上で、運用方法を検討することが重要です。
複利運用は、難しそうだけど、やってみる価値があるわね!
今回の記事では、複利の仕組みや効果、そして72の法則などについて解説しました。
💡 複利は、利息が元本に積み立てられる仕組みで、資産を効率よく増やすことができます。
💡 72の法則を活用することで、資産が2倍になるまでの期間を簡単に計算できます。
💡 複利運用は、長期的な視点での投資に適しています。


